Skittles
Over the last year or so, I’ve been very preoccupied with this claim on the back of all Skittles packets:

This started as a five-minute talk at Mathsjam, and has grown into a one-hour interactive talk that’s perfect for Sixth Formers. I currently run it at our Departmental Open Days but I’m very happy to come and deliver it at a school.
We use some combinatorics to work out how many different packets there are, some probability to think about the likelihood of finding a matching pair of packets, and then some statistics to test our hypotheses…
I now have data about 425 packets of Skittles (and counting): you can download it here if you’re interested.
Spoilers: the maths
This whole ordeal starts with the unlikely-seeming claim that no two packets of Skittles are the same. I’m willing to go along with the idea for the bigger (152g) bags, and maybe even for 45g bags (on which more later)1, but I first noticed it written on the “trick-or-treat” size bags, which are only 18g:
%picture
It seemed that in such a small bag, there couldn’t possibly be that many different variations.
After some “data gathering” %picture I established that there are either 16 or 17 Skittles in each bag.
As we can see in the image further up the page, there are five flavours of Skittle: lemon, lime, orange, red, and purple. To work out how many different ways a bag of 16 Skittles can be composed of these five flavours, we use some combinatorics.
Suppose we tip all the Skittles out, and arrange them in order, starting with purple ones and ending with green ones:
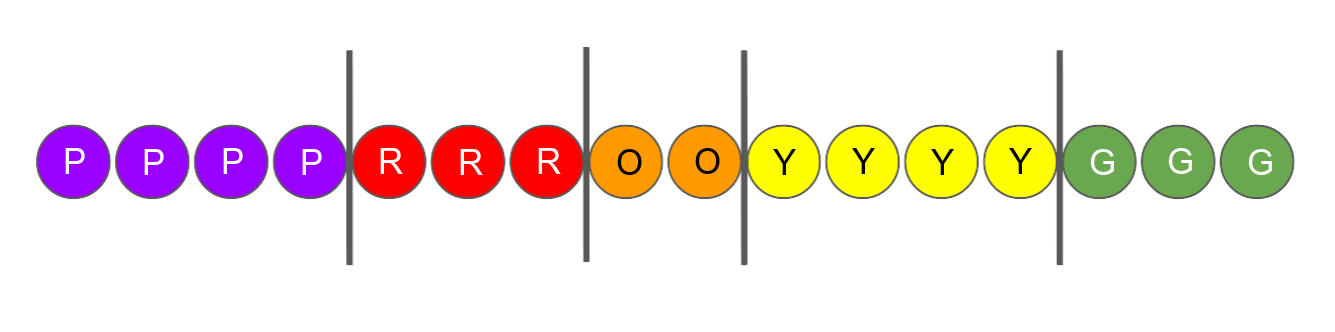
If you see them lined up in a row, you know exactly what kind of Skittles were in my packet. In fact, if you know that my plan was to go purple-red-orange-yellow-green, you don’t even need the colour version of the picture to know which Skittles I had. This black-and-white picture is enough to go on:
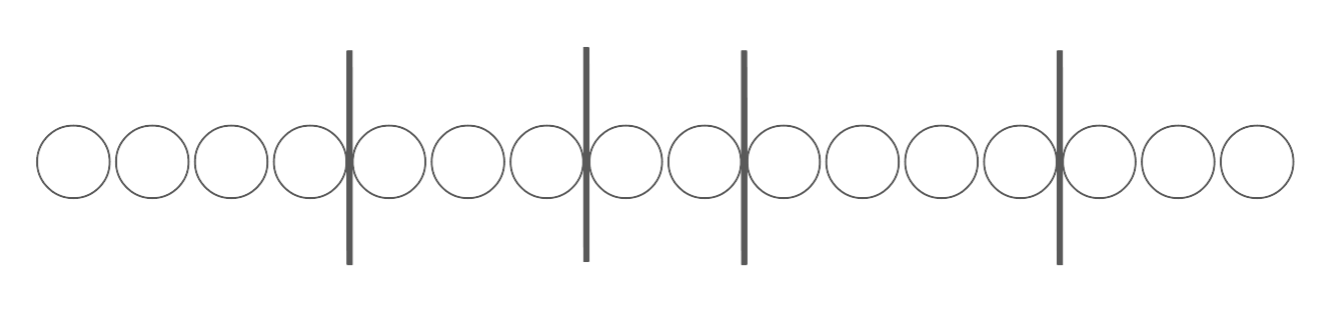
We could even go further and just write down the positions of the dividing lines: there are twenty “things” in my picture, and the fourth, ninth, twelfth, and seventeenth are dividers (all the rest are Skittles).
So if we want to work out how many different packets of Skittles there are, we can just work out how many ways there are to position my four dividing lines among the twenty things in my picture. That’s $\choose{20}{4}$! This tactic is often called stars and bars, or sheep and fences.
Okay - so if there are either 16 or 17 Skittles in my packet, there are $\choose{20}{4} + \choose{21}{4} = 10 830$ different possible packets we could find.
How long until we find two the same?
If I want to guarantee that I’ll find two packets that are the same, I’d need to open 10 831 packets - just in case there are no repeats in the first 10 830 that I look at. However, probability theory tells us that we can probably manage it much more quickly than that.
Let’s start by assuming that every packet is equally likely to come in any of the combinations. That’s quite a big ask, it turns out - but it will do for now.
If I’ve opened $n$ packets, what’s the probability that they’re all different?
When $n=1$, the probability is 1 (we can’t have two packets the same if we only open one). When $n=2$, the probability that the second one is different from the first is \(\frac{10829}{10830},\) because there are 10 829 packets “left”.
When $n=3$, the probability that all three are different is \(\frac{10 829}{10 830} \times \frac{10 828}{10 830},\) because the third packet needs to be different from the first two.
If we keep going, the probability that $n$ packets are all different is \(\frac{10 829}{10 830} \times \frac{10 828}{10 830} \times \dots times \frac{10 831-n}{10 830} = \frac{10 830!}{(10 830-n)! 10 830^n}.\)
This dips below 0.5 when $n=123$. (This is where open days come in - there are usually around 120 students and parents in the audience, and they’re all happy to eat a packet of Skittles for the sake of science.) If we can get to $n=180$ (ten multipacks, or about £30 worth of Skittles), the probability comes down to around a quarter.
Stati-Skittle analysis
But there’s an issue here: we should only get to 50% probability of finding a match when we open at least 123 packets. So how is it possible that, every time I’ve given the Skittles talk, we’ve found at least one match - and sometimes two or three?
It all comes down to our assumption: that every packet is equally likely to be any of the combinations. Thinking about it, it would be really hard to build a factory line in which “17 reds” came out as often as the well-mixed combinations like “three of each plus an extra orange.” We can do a bit of statistics to show that this assumption is not a great one, by looking at the most common colour in different packets of Skittles. The packets I’ve opened have all been pretty well-mixed: at most, we’ve had ten of the same colour of Skittle. Is that weird? Let’s think about a slightly easier question: how many times should I have seen at least fifteen of the same colour of Skittle in one packet?
We’ll start at the top: how many different ways can a packet have 17 of the same colour? Just five: they’re all purple, all red, all orange, all yellow, or all green.
How many different ways can a packet have 16 of the same colour? There are five possible 16-Skittle packets, and $5\times4=20$ different 17-Skittle packets (five options for the “main” colour, and four options for the “bonus” Skittle in each case).
Using the same logic, there are $5 \times 6 + 5 \times 4 + 5 \times 4 = 70$ different packets with 15 of the same colour (and either two more of different flavours, two more of the same flavour, or just one more).
So $70 + 25 + 5 = 100$ of the 10 830 possible packets have at least fifteen of the same colour. So we should see them about 1% of the time! Let’s set this up as a hypothesis test:
$H_0$: Every packet is equally likely to come up, and in particular about 1% of packets contain 15 or more Skittles of the same colour.
$H_1$: fewer than 1% of packets contain 15 or more Skittles of the same colour.
Under $H_0$, when we open 300 packets of Skittles, the number of packets with at least 15 Skittles of the same colour has a Binomial distribution: $N \sim \text{Bin}(300, 0.01)$.
So the probability that we don’t see any packets with at least 15 is $\mathbb{P}(N = 0) = 0.99^{300} \approx 0.049$. That is (just!) under the all-important $p=0.05$, beyond which we can reject our original hypothesis.2
So we should reject $H_0$ at the 5% significance level (and, soon, at the 1% significance level as well). Of course all of the combinations aren’t equally likely to appear - it makes much more sense to use a multinomial distribution to think about the number of each colour of Skittle in a packet. But that’s a whole different talk.